Embark on an illuminating journey with the polygon angle-sum theorems answer key, a comprehensive guide to understanding the intricate relationships between polygons and their angles. This key unlocks a treasure trove of knowledge, empowering you to conquer the challenges of polygonal geometry with confidence.
Delve into the fascinating world of polygons, where we explore their diverse types, unravel the secrets of their interior and exterior angles, and witness the practical applications of angle-sum theorems in real-world scenarios. Prepare to be captivated as we unlock the mysteries of polygonal geometry, one angle at a time.
Polygon Basics
A polygon is a closed figure in a plane bounded by straight line segments. Polygons can be classified into different types based on the number of sides they have. Some common types of polygons include:
- Triangle (3 sides)
- Quadrilateral (4 sides)
- Pentagon (5 sides)
Polygons can also be classified as regular or irregular. A regular polygon has all sides and angles equal, while an irregular polygon does not.
Angle-Sum Theorems
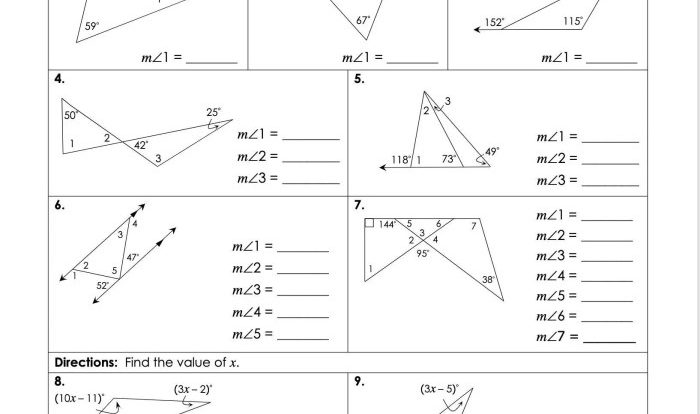
Interior Angle-Sum Theorem for Triangles
The interior angle-sum theorem for triangles states that the sum of the interior angles of a triangle is 180 degrees.
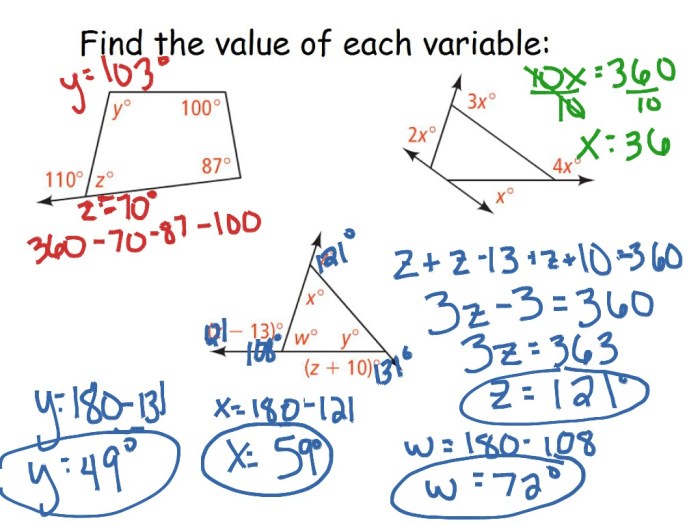
Generalization of the Interior Angle-Sum Theorem for Polygons with n Sides
The interior angle-sum theorem can be generalized for polygons with n sides. The sum of the interior angles of a polygon with n sides is given by the formula:
(n
- 2)
- 180 degrees
Exterior Angle-Sum Theorem
Definition of the Exterior Angle of a Polygon, The polygon angle-sum theorems answer key
The exterior angle of a polygon is the angle formed by one side of the polygon and the extension of the adjacent side.
Exterior Angle-Sum Theorem for Polygons with n Sides
The exterior angle-sum theorem for polygons with n sides states that the sum of the exterior angles of a polygon with n sides is 360 degrees.
Applications of Angle-Sum Theorems: The Polygon Angle-sum Theorems Answer Key
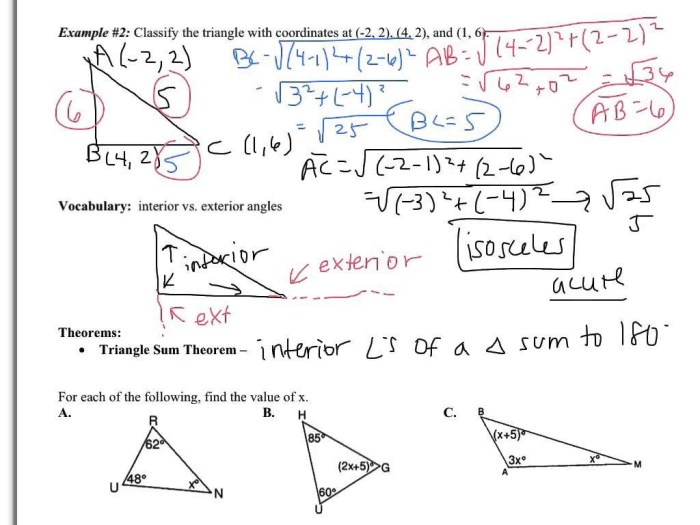
Determining the Sum of Interior Angles for a Given Polygon
The angle-sum theorems can be used to determine the sum of the interior angles for a given polygon. For example, the sum of the interior angles of a pentagon is (5 – 2) – 180 = 540 degrees.
Finding the Measure of Each Interior Angle for a Regular Polygon
The angle-sum theorems can also be used to find the measure of each interior angle for a regular polygon. For example, each interior angle of a regular hexagon is 180 / 6 = 120 degrees.
Helpful Answers
What is the interior angle-sum theorem for polygons?
The interior angle-sum theorem states that the sum of the interior angles of an n-sided polygon is (n-2) x 180 degrees.
How do I find the measure of each interior angle for a regular polygon?
To find the measure of each interior angle for a regular polygon, divide the interior angle sum by the number of sides.
What are some real-world applications of angle-sum theorems?
Angle-sum theorems find applications in architecture, engineering, and construction, where they are used to determine the angles of roofs, bridges, and other structures.