Unit 4 congruent triangles classifying triangles – Unit 4: Congruent Triangles and Triangle Classification delves into the fundamental concepts of triangle congruence and the various methods used to classify triangles. This exploration provides a solid foundation for understanding the properties and applications of congruent triangles in geometry and beyond.

Through clear explanations and engaging examples, this unit equips learners with the knowledge and skills necessary to identify, classify, and apply congruence theorems to solve geometric problems effectively.

1. Introduction to Congruent Triangles

Congruent triangles are triangles that have the same size and shape. They are identical in every way, meaning that they have the same side lengths and the same angle measures. Congruence is a fundamental concept in geometry, and it is used to prove many important theorems.

The concept of congruence is based on the idea of superposition. Two triangles are congruent if they can be placed on top of each other and match exactly. This means that their corresponding sides and angles are equal.

Congruent triangles have a number of important properties. For example, they have the same area and the same perimeter. They also have the same centroid, which is the point where the medians of the triangle intersect.

2. Classifying Triangles

Triangles can be classified into different types based on their side lengths and angle measures. The most common types of triangles are:

• Equilateral triangleshave all three sides equal in length and all three angles equal to 60 degrees.
• Isosceles triangleshave two sides equal in length and two angles equal in measure.
• Scalene triangleshave no sides equal in length and no angles equal in measure.

Triangles can also be classified based on their angle measures:

• Acute triangleshave all three angles less than 90 degrees.
• Right triangleshave one angle equal to 90 degrees.
• Obtuse triangleshave one angle greater than 90 degrees.

3. Congruence Theorems: Unit 4 Congruent Triangles Classifying Triangles

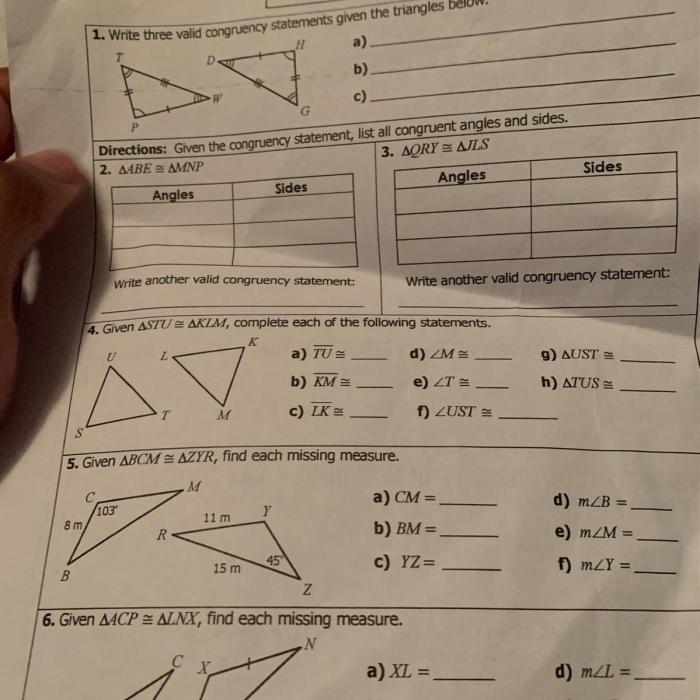
There are a number of theorems that can be used to prove that two triangles are congruent. The most common congruence theorems are:

• Side-Side-Side (SSS) Congruence Theorem: If two triangles have all three sides equal in length, then they are congruent.
• Side-Angle-Side (SAS) Congruence Theorem: If two triangles have two sides and the included angle equal, then they are congruent.
• Angle-Side-Angle (ASA) Congruence Theorem: If two triangles have two angles and the included side equal, then they are congruent.

4. Applications of Congruence

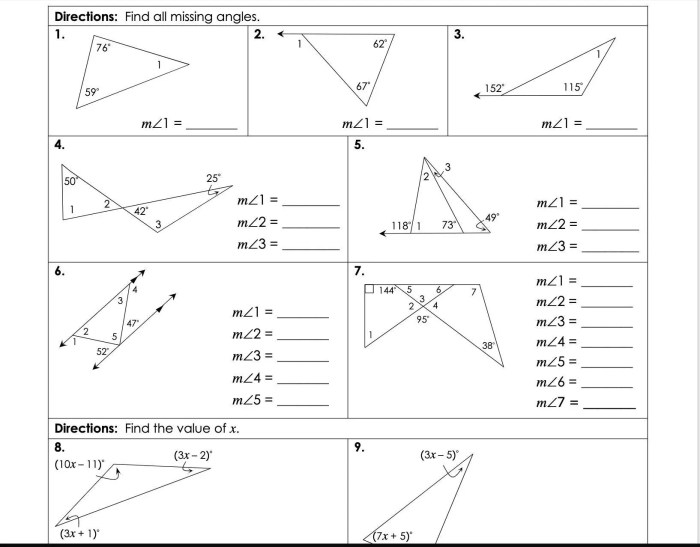
Congruence is a useful concept in geometry. It can be used to prove many important theorems, and it can also be used to solve a variety of problems.

One of the most important applications of congruence is in the construction of geometric figures. For example, a carpenter can use congruence to make sure that the sides of a table are equal in length. A builder can use congruence to make sure that the walls of a house are perpendicular to each other.

Congruence is also used in a variety of real-life applications. For example, it is used in the design of bridges, airplanes, and other structures. It is also used in the manufacture of clothing, furniture, and other products.

FAQ Corner

What is the definition of congruent triangles?

Congruent triangles are triangles that have the same shape and size, meaning their corresponding sides and angles are equal.

What are the three congruence theorems?

The three congruence theorems are the Side-Side-Side (SSS) Congruence Theorem, the Side-Angle-Side (SAS) Congruence Theorem, and the Angle-Side-Angle (ASA) Congruence Theorem.

How can congruence be applied in real-life situations?

Congruence is used in various applications, such as architecture, engineering, and design, to ensure that structures and objects are built to precise specifications.